必看秘籍 | 逻辑易混淆词语辨析——“至少”和“至多”
昭召董笑飞老师一文带你解决‘至多至少’问题
认真看完，从“双重否定 和反面矛盾”去破题 2025年管综英语全程班649元，含一对一答疑、考试大纲配套教辅、日周学习计划、录播+直播，周测月考直播答疑等，需要的学员可咨询沐颜购买微信FK3934。不必浪费几千块报各种班！ 
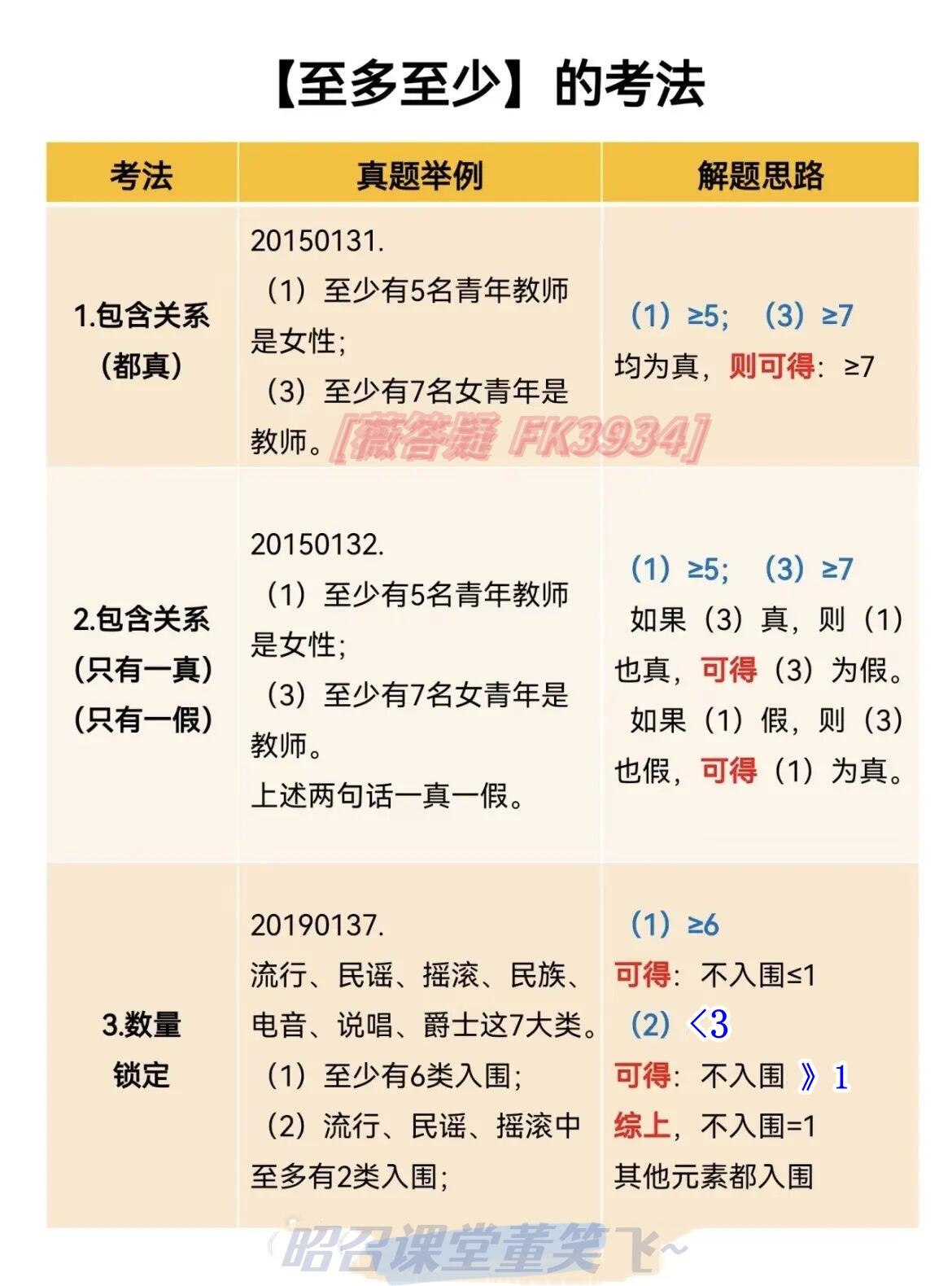
逻辑‘至多至少’总结之第一部分
在逻辑判断中，经常有一些相似的词语会影响对题目理解的准确性，而找到这些词语的区别点，理解好这些词语，能够帮助我们提升做题的正确率。今天我们就来辨析一下“至少”和“至多”。
至少
“A和B中至少有一个”，也就是在两者中，我们可以选择的数量是≥1，包含着只选择一个;以及都选择，也就是为2的可能性。所以是我们理解的“A或B”。
至多
“A和B中至多有一个”，也就是在两者中，我们可以选择的数量是≤1，包含着只选择一个;以及都不选择，也就是为0的可能性，所以是我们理解的“不能A和B同时发生”，应该理解为“非A或非B”。
例题
例：副校长：我主张王老师和邱老师中至多有一人可以被推荐为国家级教学名师候选人。校长：我不同意。
以下哪项最准确地表达了校长的意见?
A.王老师和邱老师都不可以被推荐为国家级教学名师候选人
B.王老师和邱老师中至少有一人可以被推荐为国家级教学名师候选人
C.王老师和邱老师都可以被推荐为国家级教学名师候选人
D.如果王老师可以被推荐为国家级教学名师候选人，则邱老师也可以
解析
答案：C。【解析】题干的问法是“哪项最准确地表达了校长的意见”，而校长不同意副校长的话的，则是要找副校长的话的矛盾。副校长的话“我主张王老师和邱老师中至多有一人可以被推荐为国家级教学名师候选人”，其实就是“并非王老师和邱老师都能被推荐为国家级教学名师候选人”，也可以理解为“王不入选或邱不入选”。而这句话的矛盾应该是“王老师能入选且邱老师也能入选”。
A选项，是“王老师不能入选且邱老师不能入选”，也就是两人中能入选的人为0，符合副校长的话，证明了副校长的话为真，而非校长的意见，可排除。
B选项，是“王老师能入选或邱老师能入选”，也就是两者中至少有一人能入选，包含着只一人，和都入选的可能，不必然能反应校长的话额含义，可排除。
C选项，“王老师能入选且邱老师能入选”，就是校长的话的含义。
D选项，“如果...则...”是假言命题的联结词，表示的是“王老师入选⇒邱老师入选”，而这句话不必然代表现实情况时“王老师入选且邱老师入选”，可排除。
综上，这道题应该选择C选项。
第二部分
1、共有的命题结构
从“小庄在六道题中至少答对5道题”、“射手在四次里至少射中1次”、“人体至少有道防线防住病毒”可提取出共同的命题结构：
M个事物中至少有N个是P
自然，还有一种相对应的含“至多”的命题结构：
M个事物中至多有N个是P
2、命题的等价形式转换：“至少······是”与“至多······不是”的互换
小庄在六道题中至少答对5道题=小庄在六道题中至多答错1道题
射手在四次里至少射中1次=射手在四次里至多没射中3次
人体在三道防线里至少有道防线防住病毒=人体在三道防线里至多两道防线没防住病毒
从上述这些例子里，我们很容易就能发现如下规律：
M个事物中至少有N个是P=M个事物中至多有（M-N）个不是P！！！
3、命题的否定形式转换：“至少······是”与“至多······是”的互换
-例1-
“小庄（六道题中）至少答对5道题”的否定
=并非小庄（六道题中）至少答对5道题
=小庄（六道题中）至多答对4道题。
-例2-
“射手（四次里）至少射中1次”的否定
=并非射手（四次里）至少射中1次
=射手（四次里）至多射中0次
=射手（四次里）都没有射中。
-例3-
“人体(三道防线里)至少有道防线防住病毒”的否定
=并非人体(三道防线里)至少有道防线防住病毒
=人体(三道防线里)至多零道防线防住病毒
=人体(三道防线里)没有防线没防住病毒。
从上述这些例子里，我们找到共同的“至少”与“至多”互换的规律：
“M个事物中至少有N个是P”的否定
=并非M个事物中至少有N个是P
=M个事物中至多有（N-1）个是P
“M个事物中至多有N个是P”的否定
=并非M个事物中至多有N个是P
=M个事物中至少有N+1个是P
相比于命题的这种直观明显的等价形式转换，初学者对于命题的否定形式转换规律，理解起来会有点吃力，这里再次介绍一种更直观的理解方式：
“M个事物中至少有n个S是P” ⇔“在这M个事物中，是P的S的数量≥n个”
因而，“M个事物中至少有n个S是P”的否定⇔“在这M个事物中，是P的S的数量≥n个”的否定
⇔“在这M个事物中，是P的S的数量＜n个”；
⇔“在这M个事物中，是P的S的数量≤（n-1）个”；
⇔“M个事物中至多有（n-1）个S是P”。
以上述的第一个句子为例：
“小庄在六道题中至少答对5道题”⇔“小庄在六道题中，答对题目的数量≥5个”
因而，“小庄（六道题中）至少答对5道题”的否定⇔“小庄在六道题中，答对题目的数量≥5个”的否定
⇔“小庄在六道题中答对题目的数量＜5个”
⇔“小庄在六道题中答对题目的数量≤4个”；
⇔“小庄在六道题中至多答对4道题”。
举一反三
尝试按如上方法，给出上述第二个句子和第三个句子的转换过程。
牛刀小试
分别给出如下语句的等价形式和否定形式：
（1）1500个人中至少有400个是男性。
（2）八台电脑里至多有两台能用。
（3）住着100个人的社区中的小明声称：“社区里有无症状感染者”。
（4）小庄看着面前的五篇英语阅读，感慨道：“没有一篇阅读在说人话”。
选言登场
在逻辑学里，经常有诸如如下形式的语句：
1.小周和小庄至少一人报考MBA。
2.小周和小庄至多一人报考MBA。
3.小周、小庄、小史三人里至少一人报考MBA。
4.小周、小庄、小史三人里至多两人报考MBA。
逻辑考试常常需要我们用选言命题去表示这些含有“至少”或“至多”的语句，那么这该如何入手呢？
我们先从最简单的第一个语句开始~~~
1.小周和小庄至少一人报考MBA。
= 小周报考MBA或者小庄报考MBA。
=小周报考MBA ∨ 小庄报考MBA。
然后，解决第二个语句~~~
2.小周和小庄至多一人报考MBA。
根据前面所说的，我们将其转为等价形式，即：
小周和小庄至少一人不报考MBA。
=小周不报考MBA或者小庄不报考MBA。
=ㄱ小周报考MBA ∨ ㄱ小庄报考MBA。
----------------
对于第二个还可以这么分析（这部分内容不要求掌握，只是要知道可以这么分析）：
小周和小庄至多一人报考MBA。对应于三种可能的情况：
情况一、小周和小庄都不报考MBA。
符号表示为ㄱ小周报考MBA ∧ ㄱ小庄报考MBA。
情况二、小周报考，而小庄不报考MBA。
符号表示为小周报考MBA ∧ ㄱ小庄报考MBA。
情况三、小周不报考，但小庄报考MBA。
符号表示为ㄱ小周报考MBA ∧ ㄱ小庄报考MBA。
综上，或者（小周和小庄都不报考MBA），或者（小周报考，而小庄不报考MBA） 或者 （小周不报考，但小庄报考MBA）
符号表示为：（ㄱ小周报考MBA ∧ ㄱ小庄报考MBA）（小周报考MBA ∧ ㄱ小庄报考MBA） （ㄱ小周报考MBA ∧ ㄱ小庄报考MBA）
第三个语句是第一个语句的推广~~~
3.小周、小庄、小史三人里至少一人报考MBA。
=小周报考MBA或者小庄报考MBA或者小史报考MBA。
=小周报考MBA ∨ 小庄报考MBA ∨ 小史报考MBA。
第四个语句的解决思路与第二个语句类似。
4.小周、小庄、小史三人里至多两人报考MBA。
= 小周、小庄、小史三人里至少一人不报考MBA。
=小周不报考MBA或者小庄不报考MBA或者小史不报考MBA。
=小周报考MBA 小庄报考MBA 小史报考MBA。
牛刀小试
假设任何人要么说真话，要么说假话。
1.用选言命题表示如下语句
（1）小周、小庄、小史三人里至少有一人说真话。
（2）小周、小庄、小史三人里至多两人说真话。
（3）小周、小庄、小史三人里至多两人说假话
2.试判断如下两个命题是否为矛盾关系（稍难！）
（1）“小周、小庄、小史三人里至多一人说真话”这个命题与“小周、小庄、小史三人里至多一人说假话” 这个命题
（2）“小周、小庄、小史三人里至多一人说真话”这个命题与“小周、小庄、小史三人里至多两人说真话” 这个命题
（3）“小周、小庄、小史三人里至多一人说真话”这个命题与“小周、小庄、小史三人里至少一人说真话” 这个命题
17425021720812026届考研专硕《管综逻辑》系统高分班
17425129440202026届考研专硕《逻辑概念》系统高分班
17411556383602026届考研专硕《管综数学》系统高分班
17415359742252026届考研英语（二）系统高分班
17415356970392026届考研英语（二）零基础通关班
17424768787622026届考研专硕《管综数学》零基础通关班
17424768844372026届考研专硕《管综写作》系统高分班
17425105886812026届考研专硕《王燚逻辑》零基础通关班